Đề kiểm tra giữa kì I Toán 9 - Năm học 2022-2023 - Trường THCS Trường Sơn (Có đáp án + Ma trận)

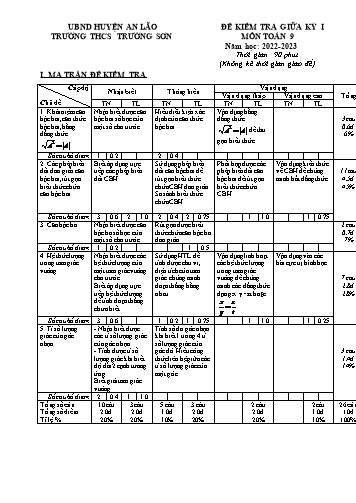
 UBND HUYỆN AN LÃO ĐỀ KIỂM TRA GIỮA KỲ I 
 TRƯỜNG THCS TRƯỜNG SƠN MÔN TOÁN 9
 Năm học: 2022-2023
 Thời gian :90 phút 
 (Không kể thời gian giao đề)
I. MA TRẬN ĐỀ KIỂM TRA
 Cấp độ Vận dụng
 Nhận biết Thông hiểu
 Vận dụng thấp Vận dụng cao Tổng
Chủ đề TN TL TN TL TN TL TN TL
1. Khái niệm căn Nhận biết được căn Hiểu điều kiện xác Vận dụng hằng 
bậc hai, căn thức bậc hai số học của định của căn thức đẳng thức 3câu
bậc hai, hằng một số cho trước. bậc hai. 2 0.6đ
 A A để thu 
đẳng thức 6%
 gọn biểu thức
 A2 A
 Số câu/số điểm 1 0.2 2 0.4
2. Các phép biến Biết áp dụng trực Sử dụng phép biến Phối hợp được các Vận dụng kiến thức 
đổi đơn giản căn tiếp các phép biến đổi căn bậc hai để phép biến đổi căn về CBH để chứng 11câu
bậc hai, rút gọn đổi CBH rút gọn biểu thức bậc hai để rút gọn minh bất đẳng thức 4.5đ
biểu thức chứa chứa CBH đơn giản. biểu thức chứa 45%
căn bậc hai So sánh biểu thức CBH. 
 chứa CBH
 Số câu/số điểm 3 0.6 2 1.0 2 0.4 2 0.75 1 1.0 1 0.75
3. Căn bậc ba Nhận biết được căn Rút gọn được biểu 2 câu
 bậc ba số học của thức chứa căn bậc ba 0.7đ
 một số cho trước đơn giản. 7%
 Số câu/số điểm 1 0.2 1 0.5
4. Hệ thức lượng Nhận biết được các Sử dụng HTL để Vận dụng linh hoạt Vận dụng vào các 
trong tam giác hệ thức lượng của tính được chu vi, các hệ thức lượng bài cực trị hình học
vuông một tam giác vuông diện tích của tam trong tam giác 
 cho trước. giác. chứng minh vuông để chứng 7 câu
 Biết áp dụng trực đoạn thẳng bằng minh các đẳng thức 2.8đ
 tiếp hệ thức lượng nhau dạng: x.y=z.t hoặc 28%
 để tính đoạn thẳng x z
 chưa biết. y t
 Số câu/số điểm 3 0.6 1 0.2 1 0.75 1 1.0 1 0.25
5. Tỉ số lượng - Nhận biết được Tính số đo góc nhọn 
giác của góc các tỉ số lượng giác khi biết 1 trong 4 tỉ 
nhọn của góc nhọn. số lượng giác của 
 - Tính được tỉ số góc đó. Hiểu công 3 câu
 lượng giác khi biết thức liên hệ giữa các 1.4đ
 độ dài 2 cạnh tương tỉ số lượng giác của 14%
 ứng. một góc. 
 Biết giải tam giác 
 vuông
 Số câu/số điểm 2 0.4 1 1.0
Tổng số câu 10câu 3câu 5 câu 3 câu 2 câu 2câu 26 câu
Tổng số điểm 2.0đ 2.0đ 1.0đ 2.0đ 2.0đ 1.0đ 10đ
Tỉ lệ % 20% 20% 10% 20% 20% 10% 100% UBND HUYỆN AN LÃO
 ĐỀ KIỂM TRA GIỮA KÌ I NĂM HỌC 2022-2023
TRƯỜNG THCS TRƯỜNG SƠN
 MÔN : TOÁN 9
 Thời gian làm bài: 90 phút
A.TRẮC NGHIỆM: (3 điểm) 
 Chọn chữ cái đứng trước câu trả lời đúng trong các câu sau:
Câu 1: Căn bậc hai số học của 4 là:
 A. 16 B. 2 C. - 2 D. 2 và -2
Câu 2 : Điều kiện xác định của biểu thức là.
A. B. C. D.
Câu 3:Giá trị của biểu thức bằng.
 A. - 1 B. 1 C. -4 D. 4
Câu4: Kết quả của phép tinh. là
 A. B. 1 - 2 C. 6 D. 1 + 2
Câu 5: Biểu thức (x 4)2 bằng biểu thức nào trong các biểu thức sau?
 A. 4 - x B. (x-4) C. x 4 D. x -4
Câu 6: Tính giá trị của biểu thức (2 3)2 4 3
 A. 13 B. 7 C. 7 4 3 D. 5
 1 1
Câu 7: So sánh giá trị của biểu thức A= và B= 2 3 .
 2 3 2 3
 D. Không so sánh 
 A. A>B B. A<B C. A=B
 được
Câu 8: Trong các đẳng thức sau, đẳng thức nào sai?
 A. ( 3 2)2 3 2 B. 50 5 2
 1
 C. (3 10) D. x y y x xy( x y) (với x,y 0 )
 3 10
Câu 9: Tìm giá trị của x biết x2 9 4
 A. x 5 B. x=5 C. x= -5 D. x=25
 Câu 10: Ở hình 1: 
 A
 Theo hệ thức lượng trong tam giác vuông ta có:
 A)AC2 =BH.BC B) AC2 =CH.BC 
 2 2 2 2 C
 C)AC =AB +BC D) AC =CH.HB B
 H Hình 1
 Câu 11: Ở hình 1 ta có SinB 
 AC AC AH AH
 A). B). C). D).
 HC AB AB BC
 Câu 12: Ở hình 1 ta có AB =
 A). BC.cosB B). BC.cosC C). AC.tanB D). AC.cot C
 Câu 13: Trong hình vẽ 2. Biết AH = 5cm; góc B = A
 600 thì độ dài BH = ?
 5 1
 5 3 3
 A/ B/ C/ D/ 5cm
 3 3 Hình 2 0
 60 m C
 Câu 14: Cũng trong hình vẽ 2 thì độ dài cạnh HC là: B
 H
 5 1
 A/ 5 3 B/ C/ D/ 3
 3 3
 Câu15:
 Tính: cos2 200 cos2 400 cos2 500 cos2 700 ta 
 được
 A. 1 B. 2 C. 0 D. -1
B: TỰ LUẬN : (7 điểm)
Bài 1(1.5 điểm) . Rút gọn biểu thức 
 2 5 5 1
a) 20 2 45 80 125 . b. (3 5)2 5
 5 1 5 5
 3 3 3 3
c. 2 64 125 5 8
 x x x - 4
Bài 2(1,5điểm)Cho biểu thức: P = .
 x 2 x 2 4x
 a) Tìm ĐKXĐ của P
 b) Rút gọn biểu thức P.
 c)Tìm x để P < 3
 2
Bài 3(3,0 điểm)Cho tam giác ABC vuông tại A, đường cao AD. Gọi E và F lần lượt 
là hình chiếu của D lên AB, AC.
 a. Giải tam giác ABC biết AB=4cm, góc C=300
 b. Chứng minh EF=AD
 c. Chứng minh AE.AB=AF.AC
 d. Khi độ dài đường cao AD không đổi, tìm điều kiện của tam giác ABC để 
diện tích tam giác DEF là lớn nhất.
Bài 4(1,0 điểm)
a) Cho ba số x, y, z thỏa mãn yz > 0. Chứng minh rằng x2 yz 2x yz . Dấu “=” 
xảy ra khi nào?
b)Cho x, y, z là ba số dương thoả mãn x + y + z =3. Chứng minh rằng:
 x y z
 1.
x 3x yz y 3y zx z 3z xy
 -------------Hết-------------- HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA GIỮA KÌ I 
 MÔN : TOÁN LỚP 9
A: PHẦN TRẮC NGHIỆM KHÁCH QUAN:(3 ĐIỂM)
Mỗi câu đúng được 0,2 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
 Đápán B B D C C B A A A B C A B A B
B: TỰ LUẬN: (7 ĐIỂM)
BÀI ĐÁP ÁN ĐIỂM
1.a Rút gọn biểu thức
 2 2
 a) 20 2 45 80 125 4.5 2 9.5 16.5 25.5 0,25
 5 5
 2 5 6 5 4 5 2 5 0,25
 6 5
1.b 5 5 1 5( 5 1) 1 0,25
 b) (3 5)2 5 3 5 25.
 1 5 5 1 5 5 0,25
 3 5 5 5 3 5
1.c 2 3 64 3 125 5 3 83 2 3 ( 4)3 3 53 5.8 0,25
 2.( 4) 5 5.8 27 0,25
2.a,b a) ĐKXĐ : x>0 và x 4 0,25
 x x x-4
 .
 x 2 x 2 4x
 x 2 x x 2 x x-4 0,25
 b)Rút gọn P .
 x 4 4x
 2x
 4x 0,25
 x 0,25
 3 3
2.c c)Tìm x để P < x <
 2 2
 0,25
 x < 9
 4
 0<x < 9
 4 0,25
3 Hình vẽ:
 A
 F
 F
 0,25
 C
 D
3.a a) Giải tam giác ABC
 B
 Có Bµ Cµ 900 Bµ 900 300 600 0,25
 0,25
 B BÀI ĐÁP ÁN ĐIỂM
 AB AB 4
 Có sin C BC 8cm
 BC sin C sin 30
 0,25
 AB AB 4
 Có tan C AC 4 3cm
 AC tan C tan 30
 3.b b) Xét tứ giác AEDF có 
 µ 0
 A 90 (tam giác ABC vuông tại A) 0,25
 Eµ 900 (E là hình chiếu của D trên AB)
 Fµ 900 (F là hình chiếu của D trên AC)
 => Tứ giác AEDF là hình chữ nhật 0,25
 => EF=AD (t/c đường chéo) 0,25
3.c c) - xét tam giác ADB vuông tại D, đường cao DE có:
 AE.AB=AD2 (HTL trong tam giác vuông)
 - xét tam giác ADC vuông tại D, đường cao DF có:AF.AC=AD2 0,25
 (HTL) 0,25
 Vậy AE.AB=AF.AC (cùng bằng AD2)
 d) Ta có diện tính tam giác DEF bằng một nửa diện tích hình chữ 0,25
 nhật AEDF. Nên diện tích tam giác DEF lớn nhất khi hcn AEDF có 
 diện tích lớn nhất. 0,25
 AE2 AF2 EF2 AD2
 S AE.AF 
 AEDF 2 2 2
 Vì AD không đổi nên S hcn AEDF lớn nhất khi AE=AF.
3.d Mà AE.AB=AF.AC => AB=AC. 0,25
 Vậy tam giác ABC là tam giác vuông cân.
 2
4a a) Ta có x2 yz 2x yz x2 2x yz yz 0 x yz 0 
 0,25
 luôn đúng với mọi x, y, z và yz > 0. Dấu “=” khi x2 = yz.
4b b/ Ta có: 3x + yz = (x + y + z)x + yz 
 = x2 + yz + x(y + z) x(y z) 2x yz 0,25
 => 3x yz x(y z) 2x yz x( y z) (theo câu a) 
 => x 3x yz x( x y z)
 x x
 (1)
 x 3x yz x y z
 y y
 Tương tự ta có: (2), 
 y 3y zx x y z
 z z
 (3)
 z 3z xy x y z BÀI ĐÁP ÁN ĐIỂM
 x y z
 Từ (1), (2), (3) ta có 1
 x 3x yz y 3y zx z 3z xy
 0,25
 Dấu “=” xảy ra khi x = y = z = 1
 0,25
 Các cách làm khác đúng vẫn cho điểm tối đa câu đó.
Xác nhận của BGH Xác nhận của tổ CM Người ra đề - Nhóm toán 9
 Nguyễn Thị Yến Lê Thị Lý
 Phạm Thị Hoa
 Nguyễn Thị Yến